直线斜率,又称为角系数,它表示的是一条直线相对于横轴的倾斜程度。当直线斜率的绝对值越大时,表示直线相对横轴的倾斜程度越大,即直线与横轴之间的夹角(锐角)越大;当直线斜率的绝对值越小时,表示直线相对横轴的倾斜程度越小,即直线与横轴之间的夹角(锐角)越小。

没错,直线斜率是有符号性质的,也可以说是它的方向,当直线过第一、三象限时,直线斜率是正数,当直线过第二、四象限时,直线斜率是负数。因此在分析直线相对于横轴的倾斜程度,即直线与横轴的夹角时,必须以直线斜率的绝对值,以及夹角中的锐角为准。否则有可能出现问题。比如说“斜率越大,直线和横轴间的夹角越大”,这显然是错误的。因为斜率是负数时,在直线的右侧,直线和横轴间的夹角是一个负数。
这方面分析起来有点绕,但是想真正理解直线斜率的内涵,就必须先把自己绕进去,然后再靠自己的理解,把自己绕出来。不绕进去,你永远不可能知道其中的真理,绕不出来,你也掌握不了这个真理。
当然,直线斜率的实质是直线和横轴间的右上夹角的正切值。这是直线斜率在“数”方面的真相。上面讲的是直线斜率在“形”方面的真相。只有数形结合,才能真正理解直线斜率的实质。
如下图,我们一般记直线斜率为k,直线与横轴间的右上夹角为θ,则k=tanθ。左图直线过第一、三象限,θ是锐角,因此k>0;右图直线过第二、四象限,θ是钝角,因此k<0;而当θ是直角时,直线斜率不存在。
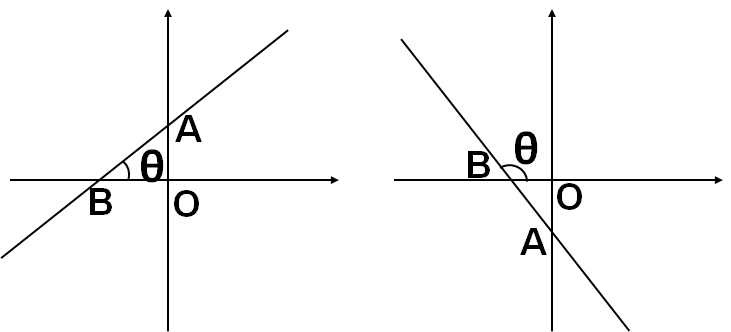
接下来就是求直线斜率的问题了。上图中右图的直线斜率可以通过OA和OB的比值求得,即k=OA/OB。但若你以为左图的直线斜率也可以用k=OA/OB求得,那就大错特错了。因为线段OA和OB都是正数,求得的k一定是正数,而上面我们讲过,当θ是钝角,k<0,这就产生了矛盾。所以前面老黄才分析了那么多关于直线斜率“数形结合”的内容。
正确的写法不只一种,但都必须建立在理解的基础上,可以写成|k|=OA/OB,则对两种情形都成立,因为k的绝对值一定是正数。也可以写成k=tanθ,左图tanθ=OA/OB,右图tanθ=-OA/OB。或者引入位移的概念,k=OA/BO,这里的OA,BO表示的不是距离,而是位移。BO从小到大为正位移,OA从大到小,为负位移。
或者k=-yA/xB。这个式子是来自于求斜率的另一个重要公式。已知直线上两点(x1,y1), (x2,y2),则直线斜率k=(y1-y2)/(x1-x2)或k=(y2-y1)/(x2-x1)。由于直线AB上有两点A(xA,yA),B(xB,yB),所以kAB=(yA-yB)/(xA-xB),而xA=0, yB=0,因此kAB=-yA/xB.
求直线斜率在求直线解析式的题目中非常重要,所以关于直线斜率的公式,不仅都要记牢,而且都要好好理解。到了高数学习导数的知识时,我们还有更多关于直线斜率的知识要去掌握,基础薄弱的同学,会觉得很难,基础扎实的同学,会因为自己又打开了新的一扇知识的窗口而兴奋不已。