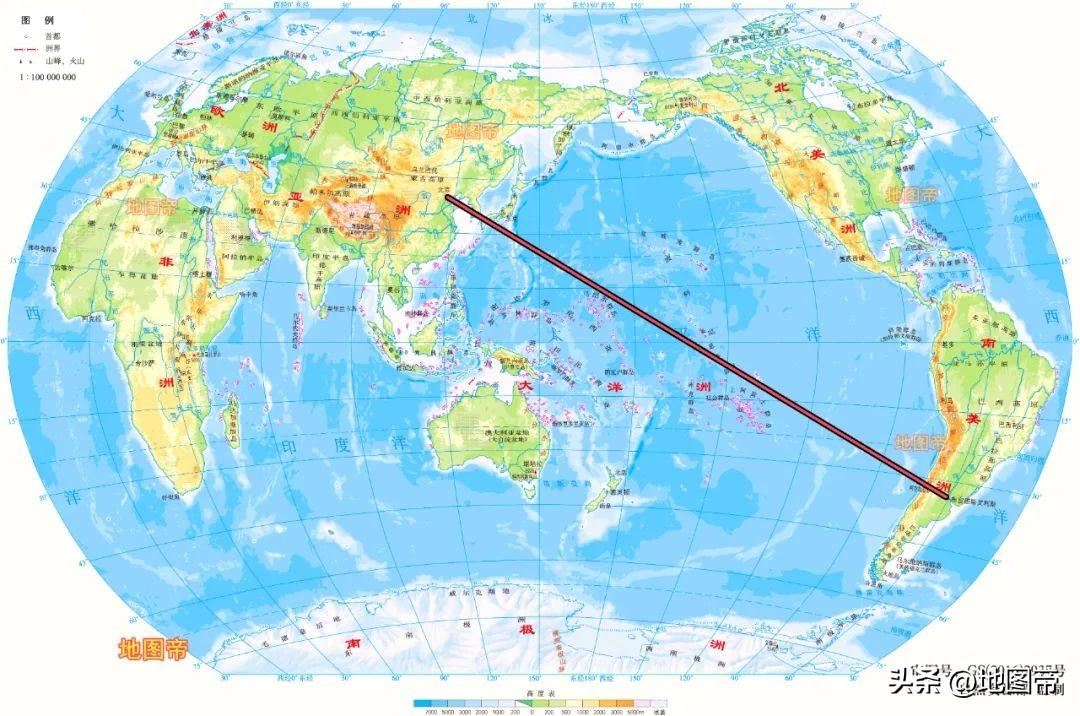
下面我们看到一个不规则的六边形，有五个已知的角，其中一个未知的角。

我们如何得到未知的角度?

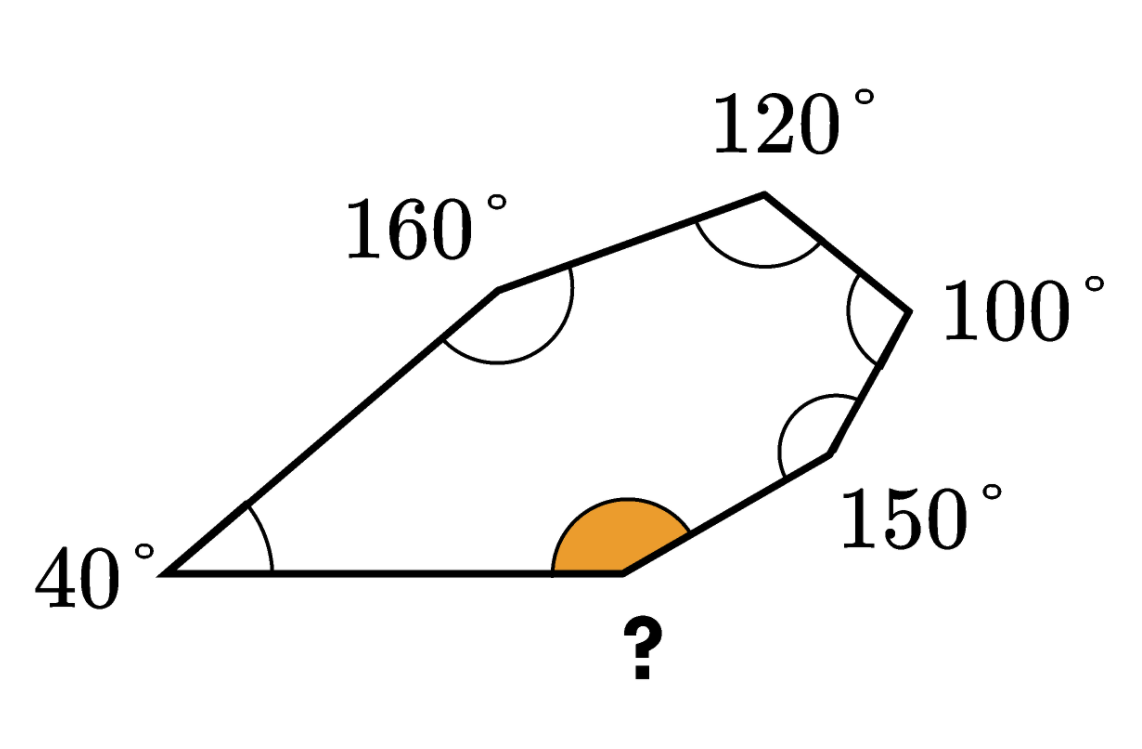
将一个较大图形拆分成多个小图，可以使问题更容易解决。

让我们把这个六边形分成几个三角形。

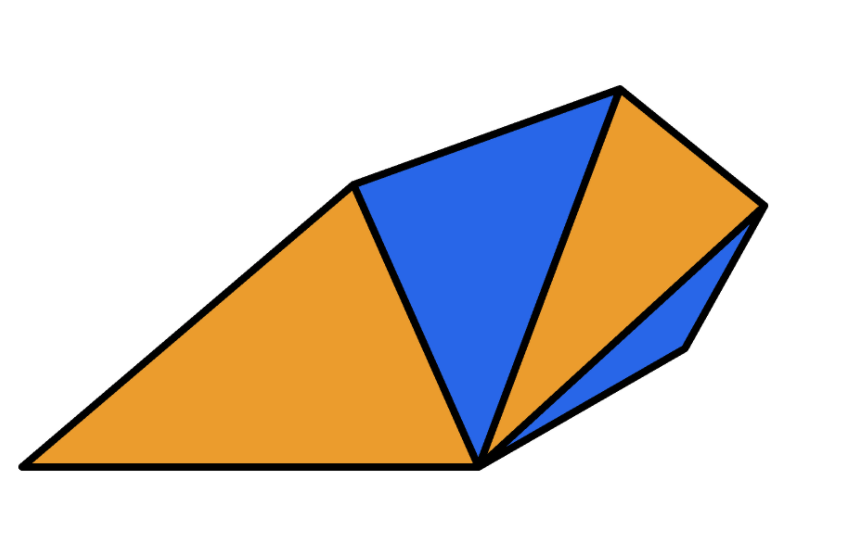
三角形的一个有用的特性是它们的角和:无论三角形的形状，它的内角的和总为180°。

我们把这个六边形分成4个三角形，每个三角形的内角都被测得和为180°。

所有三角形的内角之和为180°x4=720°。

六角形的每个内角都是由四个三角形的角构成的，因此六角形的内角之和也为720°∘

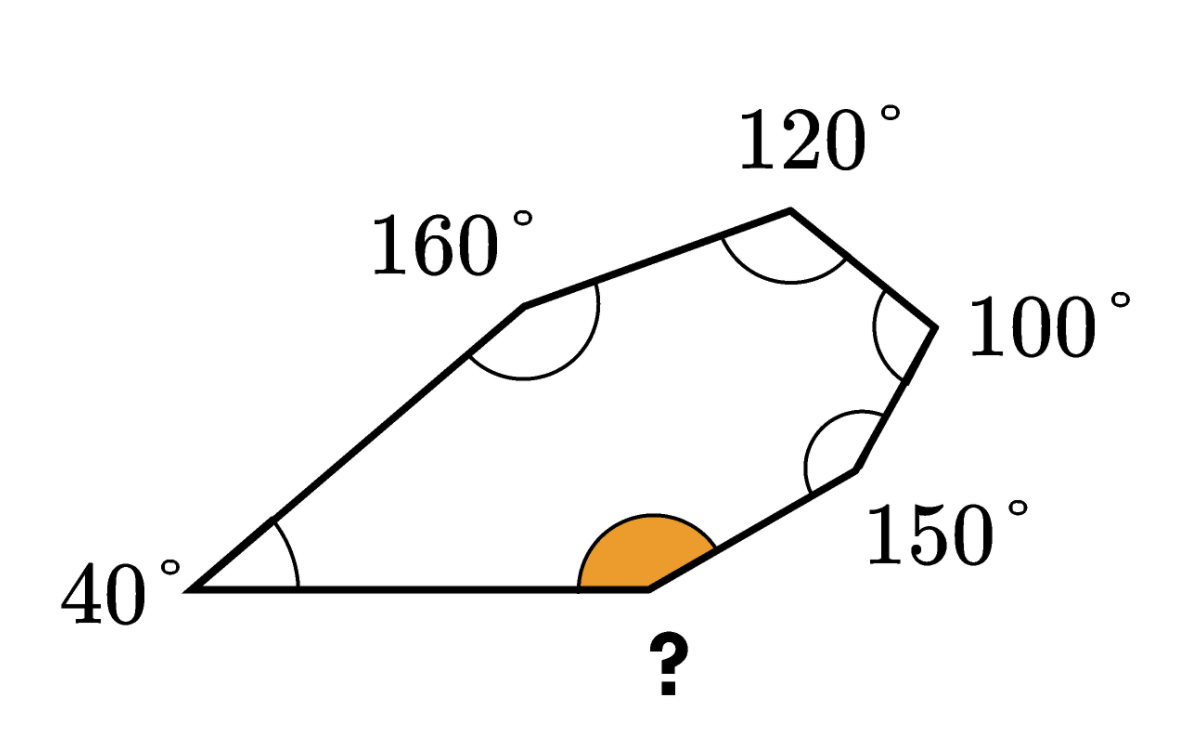
一直角度的大小之和为40°+160°+120°+100°+150°=570°

这意味着未知角度必须具有720°-570°=150°。

我们可以使用类似的方法来找到任何多边形的内角度之和。