性质:等腰三角形的顶角角平分线、底边上的中线和底边上的高线互相重合,
简称“等腰三角形三线合一”
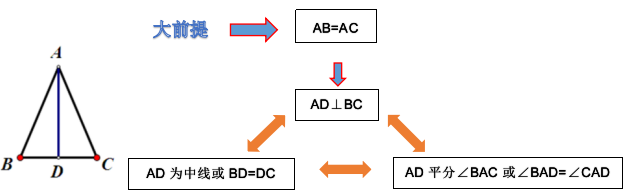
注:(1)此性质也适用于等边三角形;
(2)等腰三角形的三线中,已知其中一线,可推出另外两线成立。
反之成立吗?
(1)BD=DC,AD⊥BC,那么AB=AC是否成立?
(2)∠BAD=∠CAD,AD⊥BC,那么AB=AC是否成立?
(3)∠BAD=∠CAD,BD=DC,那么AB=AC是否成立?
答案是成立的。
例题:如图,AB=AC,AD=AE,证明:BD=CE(2种方法)
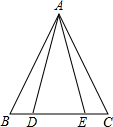
证明:
方法一:利用三角形全等
∵AB=AC,AD=AE
∴∠B=∠C,∠ADE=∠AED
∵∠ADB=180°-∠ADE
∠AEC=180°-∠AED
∴∠ADB=∠AEC
在△ABD和△ACE中
∠ADB=∠AEC,∠B=∠C,AB=AC
∴△ABD≌△ACE
∴BD=EC
方法二:利用等腰三角形的三线合一
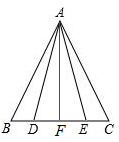
过点A作AF⊥BC
∵AB=AC,AD=AE
∴BF=CF,DF=EF
∴BF-DF=CF-EF
即BD=EC
此题用方法二证明比较简单,平时多积累方法,遇到问题时随时可以调用适合的方法解决问题。
课后练习:
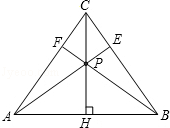
如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接
AP交BC于点E,连接BP交AC于点F.
(1)证明:∠CAE=∠CBF;(2)证明:AE=BF;